2.5. Закон Гомперца-Мейкема

Начнем рассмотрение вопроса с анализа данных по продолжительности жизни традиционного объекта генетики - плодовой мушки Drosopkila melanogaster. Если обработать данные по выживаемости большой группы одновременно родившихся генетически идентичных особей, которые содержатся в стандартных лабораторных условиях, то выявляется интересная закономерность. Оказывается, что на значительном возрастном интервале интенсивность смертности растет с возрастом по закону геометрической прогрессии (экспоненциально, в соответствии с формулой Гомперца). На рис. 2 приведена зависимость логарифма интенсивности смертности от возраста дрозофил, которая с точностью калибровочного графика ложится на прямую линию. Действительно, коэффициент корреляции между логарифмом интенсивности смертности и возрастом достигает 0,999 при 11 точках в зависимости. Та же самая закономерность справедлива и для самцов крыс линии Вистар (рис. 3).

Рис. 2. Зависимость логарифма интенсивности смертности от возраста дрозофил. Рассчитано и построено на основании таблицы выживания 2400 самок Drosophila melanogaster линии Canton-S, опубликованной в работе [Hall, 1969]. При расчете интенсивности смертности был выбран трехдневный возрастной интервал

Иногда приходится слышать возражения, что подобная линейность ничего удивительного не представляет, поскольку многие зависимости в логарифмическом масштабе выглядят как прямые. Рис. 4 содержит ответ на это замечание. На нем приведена зависимость логарифма риска гибели от возраста самок крыс линии Вистар. На том же графике пунктиром приведена теоретическая зависимость, рассчитанная для случая, если бы распределение по срокам жизни лабораторных крыс следовало нормальному закону с той средней и дисперсией, которые наблюдаются в эксперименте. Видно, что экспериментальные точки гораздо лучше ложатся на прямую линию, чем на теоретическую зависимость, проведенную пунктиром, что еще раз подтверждает необоснованность использования нормального закона для описания распределения по срокам жизни.

Рис. 3. Зависимость логарифма интенсивности смертности от возраста лабораторных крыс. Рассчитано и построено на основании таблицы выживания 2113 самцов крыс линии Wistar, опубликованной в работе [Schlettwein-Gsell, 1970]. При расчете интенсивности смертности был выбран 50-дневный возрастной интервал

Приведенные выше примеры экспоненциального роста интенсивности смертности с возрастом являются далеко не единственными. Так, для тех же лабораторных дрозофил было найдено восемь таблиц смертности, построенных для популяций с исходной численностью свыше 1000 особей [Hall, 1969; Pearl, Parker, 1921]. При обработке этих таблиц оказалось, что во всех случаях наблюдается линейный рост логарифма интенсивности смертности с возрастом, о чем можно, в частности, судить по высоким значениям коэффициента корреляции между переменными (г = 0,97-0,99, табл. 4).

Рис. 4. Зависимость логарифма интенсивности смертности от возраста лабораторных крыс; теоретическая зависимость для случая нормального распределения продолжительности жизни (пунктир). Рассчитано и построено на основании таблицы выживания 2050 самок крыс линии Вистар, опубликованной в работе [Schlettwein-Gsell, 1970]. При расчете интенсивности смертности был выбран 50-дневный возрастной интервал

Разумеется, коэффициент корреляции является не самой лучшей мерой линейности изучаемой зависимости, поскольку его отличие от единицы может быть связано как со случайным разбросом данных, так и с систематическими отклонениями от линейности. Для большинства таблиц выживания лабораторных животных характерны низкая исходная численность популяций (менее 1000 особей) и, как следствие, большой статистический разброс данных. В этих условиях коэффициент корреляции между логарифмом интенсивности смертности и возрастом будет небольшим даже при чисто случайном характере отклонений от закона Гомперца. Следовательно, для проверки законов смертности на данных с большим статистическим разбросом необходимо использовать другие методы и показатели.

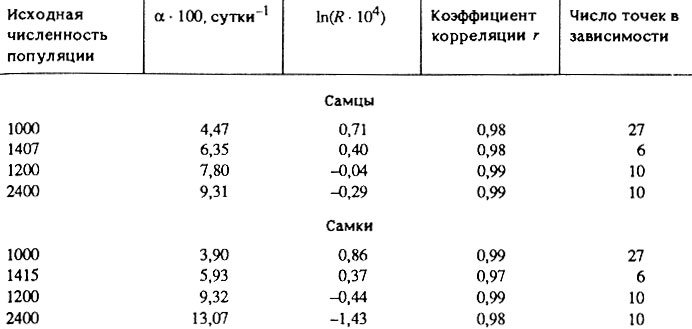
Таблица 4. Характеристики распределения продолжительности жизни Drosophila melanogaster*

^* (Рассчитано на основании таблиц выживаемости [Pearl, Parker, 1921; 1924а; Hall, 1969]. Значения параметров Гомперца (R и а) определены методом наименьших квадратов в координатах ln(μ_x) + x. Для расчета интенсивности смертности был выбран шестидневный интервал. Возрастной диапазон линеаризации составлял 28-55 дней, r - коэффициент корреляции между логарифмом интенсивности смертности и возрастом лабораторных дрозофил.)

В 1979-1980 гг. был предложен метод проверки адекватности законов смертности по неточным данным [Гаврилов, 1980; Гаврилова и др., 1979]. Применительно к формуле Гомперца метод состоит в следующем. Если распределение продолжительности жизни действительно описывается данной формулой, то зависимость логарифма интенсивности смертности от возраста должна быть линейной. В этом случае отношение тангенса угла наклона в начальном участке изучаемой зависимости к тангенсу угла наклона в ее конечном участке равно единице. Такое отношение тангенсов было названо K-критерием [Гаврилов, 1980]. Для каждой отдельно взятой зависимости величина K-критерия может существенно отличаться от единицы, однако если такое отклонение от формулы Гомперца не является систематическим, а носит случайный характер, то центр распределения K-критерия стремится к единице при увеличении числа наблюдений.

Таким образом, проверка формулы Гомперца этим методом сводится к определению центра распределения величин K-критерия (медианы, моды или среднего арифметического), рассчитанных для возможно большего числа таблиц смертности.

Авторами данной работы совместно с канд. биол. наук В. Г. Семеновой была проведена обработка 129 таблиц выживания дрозофил, опубликованных ранее [см.: Гаврилов, 1980]. Оказалось, что центр распределения K-критерия, рассчитанный как среднее арифметическое распределения, усеченного по выбросам, составил 1,03±0,19, т. е. точно совпал с теоретическим значением (1,0), ожидаемым в случае справедливости закона Гомперца.

Разумеется, данный подход, как и любой другой статистический метод, не позволяет, строго говоря, доказать справедливость того или иного закона и тем более его единственность. В лучшем случае можно говорить о том, что предлагаемая формула не противоречит фактическим данным. Однако использование K-критерия позволяет легко и просто проверить адекватность других конкурирующих формул и обоснованно отвергнуть многие из них. В качестве примера приведем результаты проверки адекватности уже упоминавшегося закона Вейбулла.

Нами было доказано, что при любых положительных значениях параметров формулы Вейбулла теоретически ожидаемое значение K-критерия равно обратному отношению возрастов, для которых рассчитывались тангенсы [Гаврилов, 1980; Гаврилова и др., 1979]. В описанном выше случае это теоретически ожидаемое отношение составляет 1,89-2,25 (разброс связан с тем, что в 129 таблицах смертности дрозофил возрастные интервалы не всегда совпадали). Нетрудно заметить, что наблюдаемое значение центра распределения K-критерия (1,03±0,19) достоверно и сильно отличается от теоретических величин (1,89-2,25), ожидаемых в случае справедливости закона Вейбулла. Таким образом, закон Вейбулла, в отличие от закона Гомперца, не согласуется с наблюдаемыми данными по продолжительности жизни дрозофил. Подобным же образом можно довольно просто и быстро провести проверку других формул на соответствие с реальными данными.

Приведенный пример показывает, что объем накопленных в научной литературе данных уже достаточен для строгой проверки конкурирующих формул и соответствующих им представлений о механизмах, определяющих продолжительность жизни. При этом в свете новых данных "старый" закон Гомперца не только не утратил своего значения, но и оказался значительно более конкурентно-способным, чем целый ряд более "молодых" и модных формул. Справедливость закона Гомперца отмечена не только для дрозофил и крыс, но также и для нематод [Johnson, 1987], головной вши [Гаврилов, 19846] (рис. 5), комаров [Гаврилов, 1980], мышей [Kunstyr, Leuenberger, 1975], лошадей [Strehler, 1962] и горных баранов [Гаврилов, 1980].

Рис. 5. Зависимость логарифма интенсивности смертности от возраста головной вши. Рассчитано и построено на основании таблицы выживания 400 самцов головной вши Pediculus humanus L., опубликованной в работе [Evans, Smith, 1952]. При расчете интенсивности смертности был выбран четырехдневный возрастной интервал

Естественно, возникает вопрос, с чем связана такая широкая применимость закона Гомперца для столь разных видов, как дрозофила и лошадь? Может быть, для этого закона существуют аналогии и в неживой природе? Оказывается, что такие аналогии действительно существуют. В частности, японский исследователь Касе [Kase, 1953] изучал "выживаемость" двухсот образцов резины при увеличивающихся нагрузках. Оказалось, что интенсивность разрывов резины экспоненциально растет с увеличением нагрузки, выраженной в ^кГ/_см². Эта же закономерность наблюдается при исследовании электрического пробоя масла в условиях повышающейся напряженности электрического поля [см.: Гумбель, 1965]. Таким образом, выявленная закономерность настолько широко распространена, что следует искать какое-то самое общее ее теоретическое обоснование.

Такое обоснование, оказывается, уже существует и дано в статистике экстремальных значений. В этом разделе теории вероятностей распределение с экспоненциально растущей интенсивностью отказов (в частном случае - интенсивностью смертности) выводится как предельное распределение и называется первой асимптотической функцией распределения наименьших значений [Гумбель, 1965]. Таким образом, данная закономерность имеет столь же строгое теоретическое обоснование, как, например, всем хорошо известный нормальный закон распределения. Следовательно, эта закономерность по широте своей применимости и строгости теоретического обоснования, несомненно, может быть признана фундаментальной.

В тех случаях, когда наблюдается отклонение от закона Гомперца, необходимо иметь в виду следующее. Наряду с факторами смертности, действие которых зависит от возраста, существуют ситуации, летальный исход в которых неизбежен для любого, даже самого здорового организма (например, катастрофы, несчастные случаи, острые инфекции и отравления). Иначе говоря, наряду с экспоненциально растущей компонентой смертности, обусловленной старением, должна существовать не зависящая от возраста компонента, связанная с экстремальными ситуациями.

Формально-математически это представление можно сформулировать как принцип суммы двух типов смертности. Согласно этому принципу, общая интенсивность смертности от всех причин является суммой двух неотрицательных слагаемых, одно из которых от возраста не зависит:

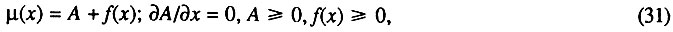
где 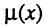- интенсивность смертности в возрасте x (имеющая смысл относительной или удельной скорости гибели); A - не зависящая от возраста компонента смертности, названная нами фоновой компонентой смертности; f(x) - зависящая от возраста компонента смертности. Как видно из предыдущего, возрастная компонента смертности является экспонентой. В частном случае, когда фоновой смертностью можно пренебречь (например, в хороших условиях лаборатории), общая интенсивность смертности экспоненциально растет с возрастом, т. е. по закону Гомперца.

Для тех случаев, когда фоновой компонентой смертности пренебрегать нельзя, был предложен метод линеаризации данных, основанный на их предварительном численном дифференцировании [Гаврилова, Гаврилов, 1983; Гаврилов и др., 1978]. Действительно, при дифференцировании постоянное слагаемое (фоновая компонента смертности) исчезает, и тогда логарифм приращения интенсивности смертности должен быть линейной функцией возраста:

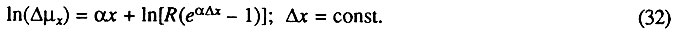
На рис. 6 приведен пример использования предложенного метода. Видно, что логарифм интенсивности смертности самок малого мучного хрущака Tribolium confusum является не линейной, а вогнутой функцией возраста (зависимость 1). Можно, однако, показать, что такое отклонение от закона Гомперца связано с недоучетом фоновой компоненты смертности. Действительно, на этом же рисунке видно, что логарифм приращения риска гибели строго линейно растет с возрастом (зависимость 2). Это означает, что закон смертности представляет собой сумму экспоненты и постоянного слагаемого (т. е. закон Гомперца-Мейкема), причем данное слагаемое больше нуля, о чем свидетельствует вогнутость зависимости 1 на рисунке. Таким образом, учет фоновой компоненты смертности позволяет объяснить наблюдаемые отклонения от закона Гомперца и дополнить наши представления о закономерностях распределения продолжительности жизни организмов.

Рис. 6. Зависимость логарифма интенсивности смертности (Z) и логарифма приращения интенсивности смертности (2) от возраста мучных жуков. Рассчитано и построено на основании таблицы выживания 400 самок малого мучного хрущака Tribolium confusum Duval, опубликованной в работе [Pearl, Miner, 1941]. При расчете интенсивности смертности был выбран 5-дневный возрастной интервал. При дальнейшем расчете приращений интенсивности смертности был выбран возрастной интервал в 30 дней

Итак, вариабельность организмов по срокам жизни во многих случаях может быть достаточно точно описана с помощью формулы Гомперца-Мейкема:

Можно показать, что данная формула удовлетворяет также всем сформулированным ранее принципам поиска и отбора конкурирующих законов распределения продолжительности жизни.

Так, формула Гомперца-Мейкема удовлетворяет принципу теоретической обоснованности, поскольку она может быть выведена из целого ряда математических моделей [Гаврилов, 1978; Гаврилов и др., 1978; Skurnick, Kemeny, 1978a; 1978b; см. также гл. 6 данной книги] и является асимптотическим распределением в статистике экстремальных значений [Гумбель, 1965].

Этот закон согласуется также с принципом суммы двух типов смертности, так как в него входят два слагаемых, одно из которых от возраста не зависит (параметр А ). Более того, непосредственный расчет показал, что оба слагаемых в формуле Гомперца-Мейкема действительно, как правило, неотрицательны [Гаврилова, 1982; Gavrilov et al., 1983]. Следовательно, этим слагаемым на самом деле можно приписывать смысл составляющих компонент смертности.

Закон Гомперца-Мейкема удовлетворяет принципу универсальности, поскольку он описывает распределения продолжительности жизни самых разных биологических видов (дрозофил, комаров, мучных хрущаков, мышей, крыс, лошадей и горных баранов), включая человека (см. гл. 3).

В соответствии с принципом локального описания отметим, что данный закон справедлив лишь для взрослых половозрелых организмов и не описывает особенности смертности на ранних этапах онтогенеза и в предельно старческом возрасте [Гаврилов, 19846; Economos, 1983].

Наконец, следует отметить, что закон Гомперца-Мейкема отвечает принципу достаточной аппроксимации при наименьшем числе параметров. Оказалось, что среди семейства трехпараметрических формул, включающего обобщенный закон Вейбулла, а также обобщенный нормальный и логнормальный законы распределения длительности жизни, формула Гомперца-Мейкема дает наилучшую аппроксимацию [Гаврилов, 1980]. Более того, установлено, что трехпараметрическое уравнение Гомперца-Мейкема аппроксимирует кривую выживания лабораторных дрозофил гораздо лучше, чем полином четвертой степени, содержащий пять параметров.

Разумеется, приведенные факты и аргументы вовсе не являются доказательством ни всеобщей приложимости закона Гомперца-Мейкема, ни тем более его единственности как фундаментального закона смертности. Вместе с тем есть все основания говорить о правомерности использования данного закона в качестве инструмента исследования в тех случаях, когда он действительно хорошо согласуется с наблюдаемым распределением по продолжительности жизни.