6.9. Проблема многообразия причин смерти и их взаимодействия [1991 Гаврилов Л.А., Гаврилова Н.С.

Большое разнообразие конкретных болезней и причин смерти порождает серьезную проблему при математическом моделировании старения, смертности и продолжительности жизни.

Возможны две крайние позиции по данному вопросу: учет всего наблюдаемого многообразия причин смерти либо его полное игнорирование. Первый подход предполагает создание множества частных моделей возрастной динамики для каждой болезни и причины смерти. Некоторые из таких моделей уже созданы [Sutherland, Bailar, 1978; Woodbury, Manton, 1983]. Несомненное достоинство подобного подхода - возможность учета специфической медико-биологической информации о конкретных механизмах возникновения и развития каждого типа патологии. Ясно, что именно такой подход создает наиболее благоприятные условия для создания полноценных содержательных математических теорий возрастной динамики отдельных болезней. Вместе с тем подобный подход не обеспечивает создания достаточно простой модели общей смертности и соответственно продолжительности жизни. Действительно, поскольку общая смертность складывается из множества отдельных причин, ее возрастная динамика должна иметь очень сложный вид, лишенный всякого смысла с точки зрения математического моделирования. Между тем анализ реальных данных показывает, что это не так. Например, возрастная динамика общей смертности обычно с достаточной точностью описывается простой трехпараметрической моделью Гомперца-Мейкема, причем при самом разном соотношении отдельных причин смерти.

Другой подход состоит в прямом моделировании возрастной динамики общей смертности так, как будто никаких отдельных причин смерти вообще не существует. В настоящее время этот подход наиболее распространен [Skurnick, Kemeny, 1978a; 1978b; Abernethy, 1979; Doubal, 1982; Economos, 1982; Witten, 1985; Piantanelli, 1986], хотя совершенно непонятно, почему можно игнорировать многообразие причин смерти ради простоты математического описания. Заявления некоторых авторов о том, что они занимаются разработкой фундаментальной математической теории продолжительности жизни, а не частными медицинскими вопросами, вряд ли можно считать исчерпывающим теоретическим обоснованием такого подхода. Весьма сомнительно, чтобы простое игнорирование вопросов возрастной патологии обеспечивало фундаментальность предлагаемых моделей продолжительности жизни.

Одно из возможных объяснений сравнительно простого поведения общей смертности связано именно с многообразием причин смерти. Действительно, если причин смерти очень много и вклад каждой из них в общую смертность сравнительно невелик, то создаются предпосылки для поиска простых предельных распределений такой суммы причин смерти. Как уже отмечалось, модель Гомперца может быть выведена из теории экстремальных значений именно как предельное распределение наименьших значений (см. разд. 6.3). Подобный подход не позволяет объяснить, однако, два других важнейших факта биологии продолжительности жизни - явление исторической стабильности возрастной компоненты смертности и компенсационный эффект смертности. В первом случае возрастная компонента смертности в модели Гомперца-Мейкема остается стабильной на протяжении XX в., несмотря на резкое уменьшение общей смертности и радикальное изменение соотношения причин смерти. Во втором случае зависимости биологической компоненты смертности от возраста, построенные отдельно для мужчин и женщин разных регионов мира, оказываются так организованы, что при экстраполяции они сходятся к одной точке, несмотря на большие половые и региональные различия в структуре причин смерти. В обоих случаях создается впечатление о прямом взаимодействии (согласованности) отдельных причин смерти, порождающем упомянутые закономерности.

Одна из гипотез, позволяющая объяснить подобные наблюдения, уже обсуждалась нами ранее (см. разд. 3.5) и связана с представлением о согласованности причин смерти. Такая согласованность может наблюдаться в том случае, если разрушение организма является многостадийным процессом, причем первые стадии разрушения, соответствующие переходу организма в состояние неспецифической уязвимости, являются самыми медленными (лимитирующими) стадиями всего процесса (Гаврилов и др., 1982]. Тогда в соответствии с принципами кинетики биологических процессов скорость этой первой стадии определяет скорость всего процесса вымирания, т. е. фактически задает величину "квоты на смерть", не зависящей от конкретных причин смерти [Там же]. Ясно, что справедливость этой гипотезы должна быть тщательно проверена. Однако очевидно и то. что игнорирование разнообразия причин смерти при математическом моделировании продолжительности жизни должно как-то обосновываться в любой предлагаемой модели.

Одним из путей решения этой проблемы может быть сопоставление повозрастных показателей интенсивности смертности от отдельных причин в различных странах мира. В случае если действительно существует общая "квота на смерть", величина которой варьирует от страны к стране, то такое сопоставление, выполненное с помощью R-техники факторного анализа [Иберла, 1982]. должно выявить существование фактора общей смертности и факторов, на общую смертность не влияющих, несмотря на их сильную связь с отдельными причинами смерти. Ниже приведены результаты, подтверждающие справедливость сделанного предположения.

Следует отметить, что в настоящее время принята прямо противоположная точка зрения о статистической независимости отдельных причин смерти. Именно эта гипотеза лежит в основе всех расчетов изменения длительности жизни при устранении отдельных причин смерти [Гревилл, 1977]. Методы оценки вклада каждой причины смерти в общую смертность также основаны на предположении о независимости причин смерти. Поэтому вопрос о том, зависимы или независимы между собой отдельные причины смерти, имеет не только принципиальное значение при построении математических моделей, но и особенно важен для определения правильной стратегии здравоохранения.

Нами была предпринята попытка проверить гипотезу статистической независимости отдельных причин смерти путем факторного анализа данных по 25 странам мира [World Health Statistics Annual, 1972; 1977; 1980; 1982; 1983]. Чтобы обеспечить сопоставимость информации, в анализ были включены материалы, составленные только в соответствии с VIII пересмотром Международной статистической классификации болезней, травм и причин смерти. В работе были использованы значения смертности в возрастной группе 55-64 года, поскольку в этих возрастах смертность от отдельных причин уже достаточно велика, а сами данные еще не искажены влиянием множественной патологии, характерной для более старших возрастов. Из публикаций ВОЗ были отобраны материалы только по тем странам и их регионам, чьи данные вызывали меньше всего сомнений в качестве регистрации причин смерти: Австралии, Австрии, Англии и Уэльсу, Бельгии, Болгарии, Венгрии, Греции, Дании, Израилю, Ирландии, Испании, Италии, Канаде, Нидерландам, Новой Зеландии, Норвегии, Португалии, США, Финляндии, Франции, ФРГ, Чехословакии, Швейцарии, Швеции, Шотландии и Японии. В большинстве случаев для каждой страны использовались данные для нескольких моментов времени (с 1972 по 1981 г.), так что общее число наблюдений составило 95. При таком числе наблюдений значения коэффициента корреляции между переменными, большие чем ±0,3, уже значимо отличаются от нуля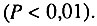

Обработка данных велась методом факторного анализа с прямым квартиминным способом вращения осей. Расчеты проводились с помощью пакета прикладных программ BMDP.

Проведенные расчеты показали полную несостоятельность гипотезы статистической независимости причин смерти. Ошибочность этой гипотезы видна уже при просмотре матрицы взаимных корреляций между отдельными причинами смерти. Так, для женской части населения наблюдается жесткая "конкуренция" между смертностью от рака желудка и смертностью от рака молочной железы: коэффициент корреляции между ними составил -0,72. Между смертностью от рака молочной железы и смертностью от туберкулеза органов дыхания также наблюдается обратная связь с коэффициентом корреляции, равным -0,71. Из положительных связей следует отметить связи между смертностью от рака желудка и смертностью от туберкулеза органов дыхания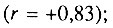

; между смертностью от пневмонии и смертностью от бронхита, эмфиземы и астмы

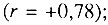; между смертностью от рака желудка и смертностью от сосудистых поражений мозга

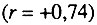(рис. 59); между смертностью от злокачественных новообразований трахеи, бронхов и легкого и смертностью от ишемической болезни сердца

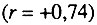; между смертностью от злокачественных новообразований пищевода и смертностью от пневмонии

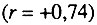. Список таких положительных и отрицательных связей между отдельными причинами смерти можно было бы продолжить.

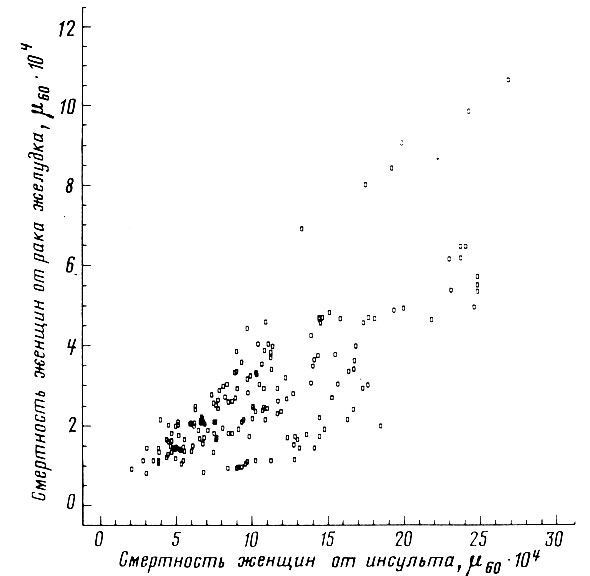
Рис. 59. Зависимость между смертностью от сосудистых поражений мозга и смертностью от рака желудка. Женщины 55-64 лет. Построено на основании данных, опубликованных Всемирной организацией здравоохранения

Сильные связи между отдельными причинами смерти наблюдаются и для мужской части населения. Из положительных коррелятивных связей следует отметить связь смертности от рака желудка со смертностью от сосудистых поражений мозга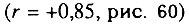

и туберкулеза органов дыхания

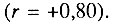. Смертность от злокачественных новообразований полости рта и глотки положительно связана со смертностью от злокачественных новообразований пищевода

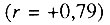и злокачественных новообразований гортани

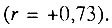Смертность от сосудистых поражений мозга положительно коррелирует со смертностью от "других нефритов и нефрозов"

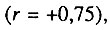а также от туберкулеза органов дыхания

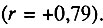Среди отрицательных коррелятивных связей особый интерес представляет "конкуренция" между смертностью от других новообразований лимфатической и кроветворной ткани и смертностью от

туберкулеза органов дыхания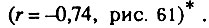

Смертность от ишемической болезни сердца конкурирует со смертностью от цирроза печени

^* (Эта закономерность представляет особый интерес, поскольку известно, что в ответ на туберкулезную инфекцию организм усиливает выработку так называемого фактора некроза опухолей, играющего ключевую роль в иммунной защите организма от злокачественных новообразований.)

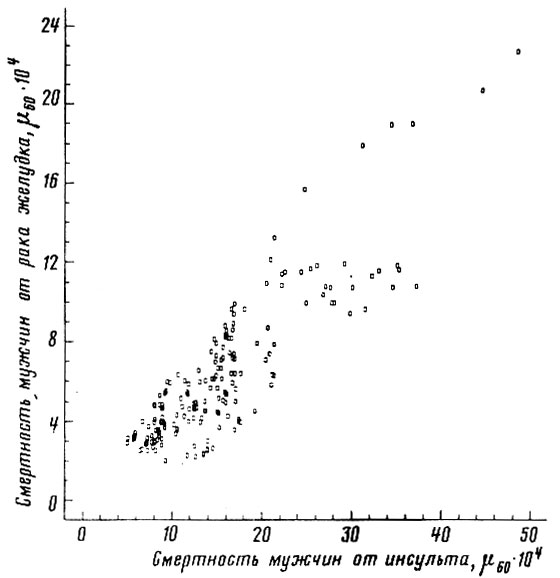
Рис. 60. Зависимость между смертностью от сосудистых поражений мозга и смертностью от рака желудка. Мужчины 55-64 лет. Построено на основании данных, опубликованных Всемирной организацией здравоохранения

Взаимодействие причин смерти приводит к парадоксальному явлению - смертность от некоторых причин смерти не оказывает никакого влияния на суммарную смертность. Например, для мужской части населения коэффициент корреляция между общей смертностью и смертностью от цирроза печени составляет всего -0,22 (связь отсутствует). Однако если исключить влияние всех остальных причин смерти, рассчитав частный коэффициент корреляции, то выявляется сильная связь между изучаемыми переменными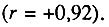

Аналогичная картина наблюдается у женщин: коэффициент парной корреляции между общей смертностью и смертностью от цирроза печени составляет всего -0,08 (связь отсутствует). При устранении же влияния всех остальных причин смерти частный коэффициент корреляции между этими переменными достигает +0,94. Получается, что вклад смертности от цирроза печени целиком компенсируется влиянием конкурирующих причин смерти (например, смертностью от ишемической болезни сердца).

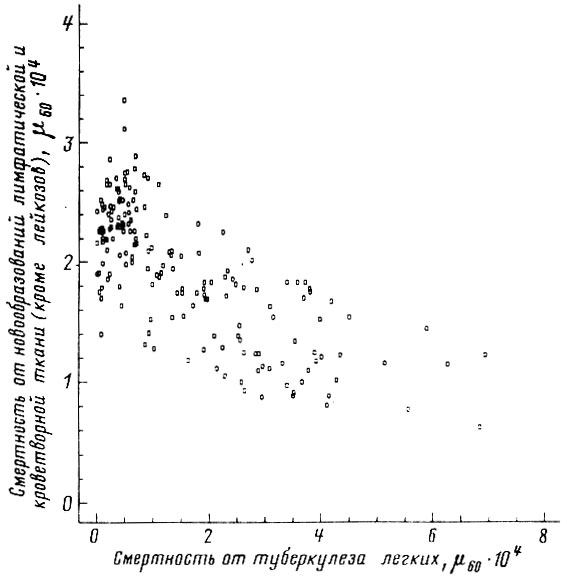
Рис. 61. Зависимость между смертностью от туберкулеза органов дыхания и смертностью от новообразований лимфатической и кроветворной ткани (кроме лейкозов). Мужчины 55-64 лет. Построено на основании данных, опубликованных Всемирной организацией здравоохранения

Более глубокий анализ обнаруженного парадокса содержится в табл. 19. В этой таблице сопоставлены теоретически ожидаемые значения коэффициентов корреляции с общей смертностью (в случае статистической независимости смертности от отдельных причин) и реально наблюдаемые значения этих же коэффициентов. Для проверки устойчивости результатов все расчеты в этой таблице проведены на расширенном массиве данных (не 132, а 179 реализаций) по смертности мужчин 55-64 лет. Можно заметить, что для таких причин смерти, как цирроз печени и "другие болезни сердца", их связь с общей смертностью действительно намного слабее ожидаемой. Напротив, такие причины смерти, как болезни артерий, артериол и капилляров, хронические ревматические болезни сердца и особенно венозные тромбозы и эмболии, проявляют парадоксально тесную связь с общей смертностью.

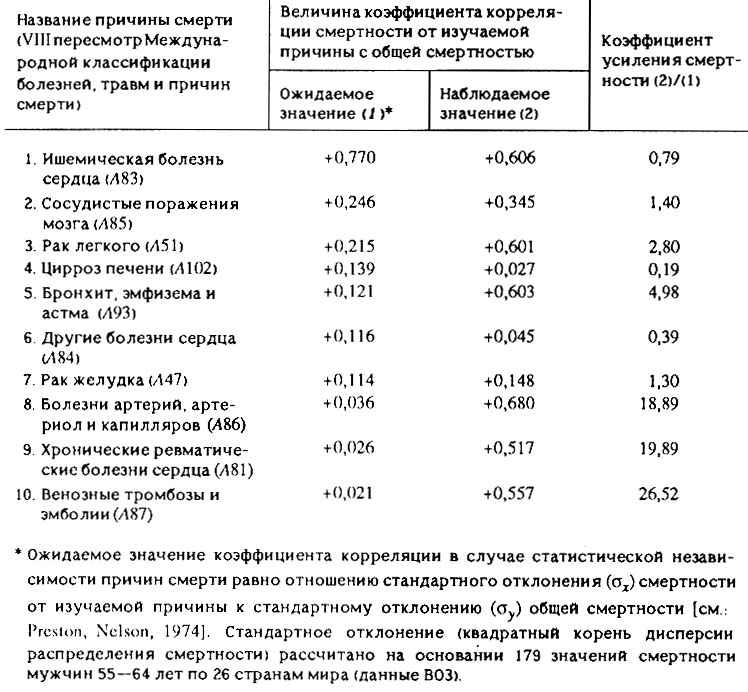
Таблица 19. Проверка гипотезы статистической независимости значений смертности от отдельных причин смертности

Приведенные данные свидетельствуют о том, что при оценке последствий устранения или снижения смертности от отдельных причин необходимо учитывать неизбежное изменение интенсивности смертности от остальных болезней. Следовательно, необходим принципиально иной подход к оценке значимости причин смерти, основанный не на величине смертности от данной причины, а на величине компоненты общей смертности, коррелирующей с данной причиной смерти. В простейшем случае новый подход сводится к определению параметров линейной регрессии:

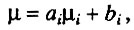
где μ - интенсивность общей смертности в изучаемой возрастной группе;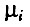

- интенсивность смертности от i-й изучаемой болезни в той же возрастной группе; параметр a_i - угловой коэффициент регрессии, названный нами коэффициентом усиления смертности для изучаемой болезни; b_i - свободный член регрессии, названный нами остаточной смертностью. Если бы причины смерти были действительно независимы, то параметр a, был бы всегда равен единице, что соответствует уменьшению смертности только от изучаемой причины. Наличие же связей между причинами смерти приводит к тому, что коэффициент усиления смертности в принципе может принимать любые значения. Например, в случае смертности женщин 55-64 лет от ишемической болезни сердца параметр a, равен 1,7. Это означает, что профилактические мероприятия, устраняющие 10 смертей от этой болезни, спасут не 10, а 17 жизней за счет дополнительного устранения ряда сопутствующих болезней. В случае смертности женщин от бронхита, эмфиземы и астмы коэффициент усиления равен 8.6, т. е. профилактика, предотвращающая всего 10 смертей от этих болезней, спасет уже 86 жизней! Таким образом, хотя смертность женщин в возрасте 55-64 лет от ишемической болезни сердца превышает ? смертность от бронхита, эмфиземы и астмы в среднем в 7-8 раз. борьба с болезнями органов дыхания может оказаться более эффективным путем снижения общей смертности. Вместе с тем следует отметить, что величина остаточной смертности для бронхита, эмфиземы и астмы составляет 7,3*10^-3 год^-1, а для ишемической болезни сердца - 6,6*10^-3 год^-1. Следовательно, полная ликвидация ишемической болезни сердца в отдаленной перспективе, возможно, привела бы к более низким значениям остаточной смертности, чем устранение бронхита, эмфиземы и астмы.

Разумеется, приведенный пример носит в основном иллюстративный характер и лишь поясняет саму идею нового подхода. Более корректным является проведение факторного анализа причин смерти и выделение факторов, сильно коррелирующих с общей смертностью. Поскольку при факторном анализе объем выборки (в нашем случае 95 реализаций) должен превышать число изучаемых переменных не менее чем в три раза [Иберла, 1982]. нами была проведена серия расчетов для различных комбинаций отдельных причин смерти. Остановимся более подробно на одном из вариантов такой обработки данных. Факторный анализ смертности мужчин от 27 причин смерти (перечислены ниже) выявил существование шести факторов, объясняющих 77% наблюдаемой дисперсии. В выделении седьмого фактора (и последующих) уже не было необходимости, поскольку он объяснял бы всего 3,5% общей дисперсии. Ниже приведена краткая характеристика выявленных факторов (их связь с анализируемыми причинами смерти), расположенных в порядке убывания объясняемой этими факторами дисперсии.

Обращает на себя внимание то, что факторный анализ позволил "опознать" все так называемые "другие" причины смерти, относящиеся к самым разным типам патологии, и установить их взаимосвязь. Самые большие значения этого фактора "других" причин смерти наблюдаются в Бельгии, а самые низкие - в Новой Зеландии.

На первый взгляд объединение этих столь разных болезней кажется странным. Известно, однако, что гипертония и язва желудка - типичные проявления стресса, причем первая болезнь способствует возникновению инсультов, а вторая - раку желудка. Наибольшие значения этого предположительно стрессорного фактора наблюдаются в Венгрии, а наименьшие - в Канаде.

Наибольшие значения этого фактора зарегистрированы в Шотландии, а наименьшие - в Японии.

Самые высокие значения данного фактора характерны для Франции, а самые низкие - для Нидерландов.

Наибольшие значения этого фактора наблюдаются в Болгарии, а наименьшие - в Венгрии.

Самые высокие значения данного фактора наблюдаются в Венгрии, а самые низкие - в Швейцарии.

Интересно отметить, что вышеперечисленные факторы оказались практически независимыми друг от друга, хотя при проведении расчетов постулат об их статистической независимости не вводился. Самое высокое значение коэффициента корреляции между факторами (фактор 1 и фактор 4) оказалось равным +0,3.

Практическое значение подобных расчетов очевидно. В самом деле, определив, какие из рассчитанных факторов тесно связаны (коррелируют) с общей смертностью, мы тем самым определяем стратегическое направление снижения смертности. Оказалось, что из шести факторов только один фактор 3 существенно коррелирует с общей смертностью!^* Таким образом, огромное многообразие болезней и причин смерти удается свести к небольшому числу их групп и выявить причины, действительно заслуживающие тщательного эпидемиологического исследования. К сожалению, детальное изложение этого подхода выходит за пределы данной книги. Возвращаясь к проблеме математического моделирования смертности и продолжительности жизни, следует отметить необходимость учета взаимодействия болезней при построении моделей частных патологий. Факторный анализ позволяет выявить такие группы болезней, взаимное влияние которых следует учитывать в первую очередь. Что касается моделирования общей смертности, то следует иметь в виду, что ее можно предсказать, зная лишь небольшую часть ее слагаемых (причин смерти), а информация об остальных причинах смерти оказывается излишней. Это явление, названное парадоксом лишних причин смерти [Гаврилов, 19896], проявляется, в частности, в том, что информации о смертности всего от двух причин (болезней артерий, артериол и капилляров; бронхита, эмфиземы и астмы) оказывается достаточно, чтобы объяснить 62% всей межпопуляционной вариации (дисперсии) общей смертности. В случае статистической независимости причин смерти эта доля объясненной дисперсии составляла бы всего 2%. Информация же о 7 причинах смерти позволяет описать межпопуляционные различия в общей смертности с точностью, соизмеримой с точностью самих данных - доля необъясненной дисперсии составляет всего 5% вместо 28%, ожидаемых в случае независимости причин смерти. Таким образом, получается, что остальные причины смерти являются "лишними" при оценке величины общей смертности.

^* (Коэффициент корреляции между фактором 3 и общей смертностью достигает +0,8, в то время как для остальных пяти факторов он оказался меньше +0,3.)

При моделировании возрастной динамики общей смертности следует также учитывать, что скорость старения (величина абсолютного возрастного прироста интенсивности смертности в когорте сверстников) тоже сопряжена с небольшим числом болезней. Наиболее тесную связь со скоростью старения проявляет смертность от гипертонической болезни, а также от болезней артерий, артериол и капилляров [Гаврилов, 1988].

Таким образом, учет взаимосвязей между отдельными причинами смерти, общей смертностью и скоростью старения является важным условием для успешного построения полноценной количественной теории продолжительности жизни.