2.2. Проблема индивидуальных различий - ключевая проблема биологии продолжительности жизни

Продолжительность жизни особей одного вида, живущих в сходных условиях, колеблется в очень широких пределах. С одной стороны, жизнь может оборваться еще до рождения. По современным данным, такова участь 70-80% оплодотворенных яйцеклеток человека, причем в большинстве случаев гибель происходит на столь ранней стадии, что обычно никем не замечается [Diamond, 1987]. С другой стороны, длительность жизни отдельных индивидуумов может значительно превышать соответствующие средние значения для всей популяции, причем абсолютной верхней границы длительности жизни, по-видимому, вообще не существует (к этому вопросу мы вернемся несколько позднее в разделе 4.2. данной книги). Но даже если отбросить все случаи гибели организма до рождения и факты удивительного долголетия, то все равно окажется, что индивидуальные различия по срокам жизни довольно велики. Например, в 1974-1978 гг. средняя продолжительность жизни мужчин в Швеции составляла 72,2 года [Befolkningsforandringar, 1970-1981]. При этом вероятность умереть в возрастном интервале 71-73 года составляла менее 6%. В других странах эта вероятность оказывается еще меньше. Можно, конечно, объяснить высокую вариабельность длительности жизни людей социальными и генетическими различиями между ними, не говоря уже о климатических и биогеохимических особенностях отдельных районов страны. Но та же картина наблюдается и в популяциях линейных лабораторных животных. Так, например, в популяции 1415 самок лабораторных дрозофил линии 107 [Pearl, Parker, 1924a] со средней продолжительностью жизни 48 дней в возрасте 43-49 дней погибло всего ИХ всех особей.

Одной из характеристик вариабельности длительности жизни может служить коэффициент ее вариации (отношение среднего квардратичного отклонения к среднему арифметическому, выраженное в процентах). Расчет этих коэффициентов на примере лабораторных дрозофил показывает, что коэффициент вариации длительности жизни составляет обычно около 35 %, достигая иногда 65 % [Семенова, 1983].

Таким образом, факт значительной биологической вариабельности длительности жизни не вызывает сомнений и требует своего объяснения, а также количественного описания. Есть еще одно обстоятельство, выдвигающее эту проблему на первый план.

В отличие от большинства других количественных признаков (например, длины или температуры тела) продолжительность жизни организма можно измерить только один раз. Этот тривиальный факт имеет далеко идущие последствия. Длительность жизни, оказывается, в принципе невозможно изучать на организменном уровне, поскольку нельзя исследовать индивидуальную динамику этого признака и определить ошибку единичного наблюдения. Поэтому единственным способом изучения продолжительности жизни остается ее популяционно-статистическое исследование при варьировании генетических и средовых факторов. Но ведь такой подход в принципе не может дать ничего, кроме информации о распределении длительности жизни в изучаемой популяции и влиянии различных факторов на это распределение! Таким образом, проблема расшифровки данных о распределении длительности жизни является ключевой для всех дальнейших исследований.

Знание закона распределения продолжительности жизни оказывается полезным уже на самых первых этапах исследования. Действительно, результаты экспериментов по выживаемости, представленные рядом значений продолжительности жизни для каждого организма, слишком громоздки для их эффективного анализа, поэтому возникает необходимость в более компактной записи результатов эксперимента. Отчасти эта проблема решается путем построения таблиц смертности (Дубина, Разумович, 1975; Коли. 1979].

Обычно таблица смертности составляется для группы одновременно родившихся индивидуумов (когорты) и описывает наблюдаемую картину смертности до того момента, когда умрет последний член этой группы. Такие таблицы смертности называются когортными и широко используются при изучении продолжительности жизни лабораторных и диких животных [Leslie, Ranson, 1940; Miller, Thomas, 1958; Pearl, Parker, 1928a].

Рассмотрим метод построения когортной таблицы смертности более подробно [Chiang, 1978]. Пусть численность когорты измеряется через одинаковые промежутки времени, равные n. Соответственно на ту же величину будет каждый раз увеличиваться и возраст членов когорты. Основными величинами, входящими в когортную таблицу смертности, являются 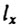- число доживших до возраста 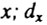- число умерших в интервале .

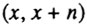Между величинами 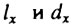существует следующее соотношение:

или

Вероятность смерти 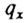в каждом возрастном интервале 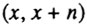можно получить делением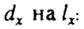

Число живущих, или, точнее, суммарное время жизни, 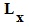в возрастном интервале 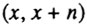обычно рассчитывается по формуле:

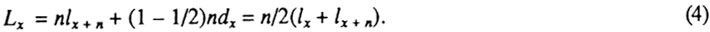
Для расчета ожидаемой продолжительности жизни необходимо начала вычислить величины 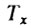для каждого возраста, которые представляют собой суммарное время жизни всех членов когорты в возрасте x и старше:

где ω - начало последнего возрастного интервала.

И наконец, ожидаемая продолжительность жизни e_x рассчитывается следующим образом:

где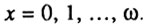

В качестве примера когортной таблицы смертности можно привести таблицу смертности имаго Drosophila melanogaster (табл. 1). На рис. 1а, б, в, г приведены типичные зависимости показателей таблицы смертности от возраста.

Таблица 1. Таблица смертности самцов имаго Drosophila melanogaster (рассчитано на основании данных [Pearl, Parker, 1924a])

Для построения таблиц смертности человека приведенным выше способом потребовался бы срок наблюдения, близкий к 100 годам, поэтому таблицы смертности людей обычно рассчитываются другим методом, который будет описан в разделе 3.1. данной книги. К настоящему времени построено большое количество таблиц смертности не только лабораторных, но также домашних [Hickey, )60] и диких [Caughley, 1966; Deevey, 1947] животных и даже растений [Solbrig, 1980]. На составление этих таблиц затрачен и продолжает затрачиваться колоссальный труд, а их значение для исследования биологии продолжительности жизни трудно переоценить. По существу, эти таблицы являются единственным экспериментальным источником для таких исследований. Между тем опубликованные таблицы смертности животных разбросаны по многим изданиям, посвященным самым разным проблемам, геронтологии, онкологии, экологии, радиобиологии и др. Далеко не во всех работах, содержащих анализ продолжительности жизни, приводятся собственно таблицы смертности. До сих пор нет исчерпывающей библиографии работ, в которых опубликованы таблицы смертности животных.

Рис. 1. Зависимость показателей таблицы смертности от возраста. а - кривая дожития (l_x); б - кривая числа умерших (d_x); в - вероятность смерти (q_x); г - средняя продолжительность предстоящей жизни (e_x). Рассчитано и построено на основании данных по выживаемости 2400 самок Drosophila melanogaster, опубликованных в работе [Hall, 1969]

В связи с этим сведение воедино опубликованных таблиц смертности животных может оказать помощь в дальнейшей разработке проблемы биологии продолжительности жизни. В табл. 2 приводится перечень опубликованных таблиц смертности животных с указанием условий проведения эксперимента.

Таблица 2. Перечень опубликованных таблиц продолжительности жизни животных (в таблице приведены лишь наиболее надежные данные, полученные для достаточно больших выборок)

Однако подход, связанный с использованием таблиц смертности, все-таки далек от совершенства. В самом деле, с одной стороны, данные таблицы (особенно полные таблицы смертности человека) все-таки остаются слишком громоздкими. Например, полная демографическая таблица дожития, в которой приводятся значения показателей за каждый год возраста, содержит не менее 80 пар значений переменных с общим объемом массива данных свыше 500 значащих цифр [Keyfitz, 1982].

С другой стороны, при построении подобных таблиц происходит некоторая потеря информации, связанная с группировкой данных по дискретным возрастным интервалам. Эта проблема могла быть решена, если бы был известен закон распределения продолжительности жизни. Например, если бы распределение организмов по срокам их жизни следовало нормальному закону, то любой сколь угодно большой массив данных о выживаемости можно было бы записать всего лишь парой чисел: величинами средней продолжительности жизни и среднего квадратичного отклонения. Таким образом, знание закона распределения длительности жизни обеспечивает наиболее компактную запись результатов эксперимента с минимальной потерей информации.

Следующая проблема, которая возникает перед экспериментатором, состоит в установлении достоверности различий выживаемости организмов при варьировании условий эксперимента. В современной геронтологии задача обычно "решается" путем механического использования методов параметрической статистики, (например, критерия Стьюдента), основанных на гипотезе о нормальном распределении продолжительности жизни. Между тем, как показали специальные исследования [Гаврилов, 1980; Семенова, 1983], распределение организмов по срокам жизни резко отличается от нормального. Результаты этих исследований, основанные на сравнении наблюдаемых и теоретических распределений с помощью χ²-критерия, приведены в табл. 3.

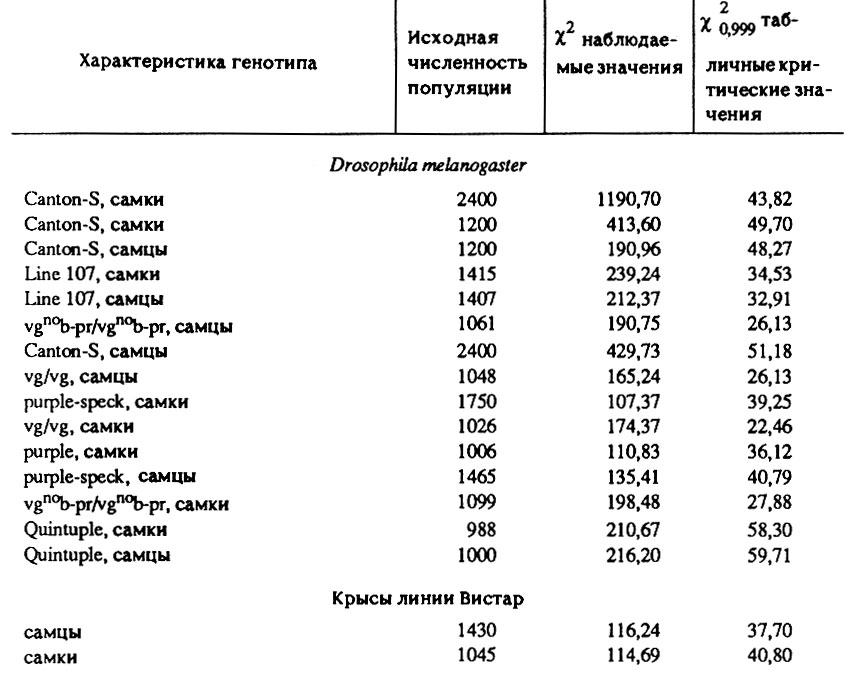
Таблица 3. Несостоятельность нормального закона для описания распределения продолжительности жизни организмов

Чтобы обеспечить высокую статистическую значимость результатов, были использованы таблицы смертности, построенные для популяций больших размеров (свыше 1000 особей). Можно заметить, что во всех случаях рассчитанные величины χ²-критерия превышали соответствующие табличные критические значения. Это означает, что нормальный закон распределения продолжительности жизни с доверительной вероятностью P>0,999 может быть отброшен как не соответствующий экспериментальным данным. Отсюда следует, что выводы, полученные с использованием методов параметрической статистики, особенно в случае малых выборок, имеют лишь видимость научной строгости и должны быть пересмотрены заново. Таким образом, знание истинного закона распределения необходимо не только для того, чтобы установить достоверность различий при минимальном числе наблюдений, но и для того, чтобы избежать ошибочных выводов.

Наконец, на заключительном этапе исследований необходимо корректно интерпретировать полученные результаты. К сожалению, в этой области в настоящее время отсутствуют единые принципы интерпретации данных по выживаемости организмов. Так, нередко делается вывод о замедлении старения на основании данных об увеличении продолжительности жизни организмов, а вещества, приводящие к такому увеличению, называют геропротекторами, т. е. защищающими от старения [Обухова, Эмануэль, 1984]. Между тем, как справедливо отмечается рядом авторов [Лэмб, 1980], далеко не всякое воздействие, влияющее на смертность и продолжительность жизни, должно влиять на старение. В противном случае в число геропротекторов следовало бы записать пенициллин и всю массу социально-гигиенических мероприятий, которые привели к резкому увеличению длительности жизни людей в XX в. Этот пример показывает, что в настоящее время необходима модель выживаемости организмов, которая была бы достаточно общей, чтобы быть признанной большинством геронтологов, но достаточно конкретной, чтобы позволять проводить единообразную интерпретацию результатов эксперимента. Нетрудно заметить, что создание подобной модели предполагает знание хотя бы самых общих свойств распределения продолжительности жизни организмов.