4.5. Компенсационный эффект смертности

В 1978 г. было обнаружено [Гаврилов и др., 1978] и в дальнейших исследованиях подтверждено [Гаврилов, 19846; Гаврилов, Гаврилова, 1979а] существование так называемого компенсационного эффекта смертности. Оказалось, что в пределах одного биологического вида значения возрастных компонент смертности согласованы между собой так, что при экстраполяции они сходятся к одной точке (рис. 29). Эта удивительная закономерность наблюдается не только для человека, но и для плодовой мушки Drosophila melanogaster (рис. 30). Видно, что пересечение в одной точке связано с тем, что снижение уровня возрастной компоненты смертности при переходе к более благополучным популяциям компенсируется увеличением относительных темпов ее роста с возрастем - отсюда и название компенсационного эффекта смертности.

Рис. 29. Явление компенсационного эффекта смертности у человека. Зависимость логарифма возрастной компоненты смертности от возраста. 1 - Индия, 1941-1950 гг., мужчины, A = 0,00787 год^-1; 2 - Турция. 1950-1951 гг., мужчины, A = 0,00316 год^-1; 3 - Кения. 1969 г., мужчины. A = 0,00531 год^-1; 4 - Сев. Ирландия, 1950-1952 гг., мужчины. A = 0,00043 год^-1; 5 - Англия и Уэльс. 1930-1932 гг., женщины. A = 0,00238 год^-1; 6 - Австрия. 1959-1961 гг., женщины. A = 0,00068 год^-1; 7 - Норвегия, 1956-1960 гг., женщины, A = 0,00055 год^-1. Рассчитано и построено на основании кратких таблиц смертности, опубликованных ООН. В качестве приближенной оценки общей интенсивности смертности использовались значения вероятности смерти в течение одного года [см.: Гаврилов, Гаврилова. 19796]

Ясно, что координаты точки пересечения уже по самому принципу своего расчета оказываются инвариантными относительно условий жизни и генетических особенностей сравниваемых популяций. Иначе говоря, они отражают самые общие (видовые) особенности распределения продолжительности жизни в популяциях одного и того же биологического вида. На этом основании координата, соответствующая возрасту пересечения всех зависимостей, была названа видовой продолжительностью жизни. Для человека данная величина составляет 95±2 года.

Рис. 30. Явление компенсационного эффекта смертности у лабораторных дрозофил. Зависимость логарифма интенсивности смертности от возраста дрозофил. 1 - дрозофилы линии Old Falmouth, New Falmouth, Sepia и Eagle Point (1000 виргинных самок); 2 - дрозофилы линии Canton-S (1200 самцов); 3 - дрозофилы линии Canton-S (1200 самок); 4 - дрозофилы линии Canton-S (2400 виргинных самок). Для расчета интенсивности смертности был выбран 6-дневный возрастной интервал [см.: Pearl, Parker, 1921; Hall, 1969]

Естественно, что при обсуждении этой интересной закономерности возникает целый ряд вопросов. Первый из них, что реально означает пересечение в одной точке и что дает знание таких видовых констант? На этот вопрос ответить довольно просто. Действительно, если известны координаты точки пересечения всех зависимостей, то достаточно знать всего одно значение возрастной компоненты смертности в том или ином возрасте, чтобы по двум точкам (одной наблюдаемой и одной расчетной видовой) провести прямую и восстановить таким образом значения возрастной компоненты смертности в других возрастных группах. Практически это означает, что по одному или двум значениям интенсивности смертности можно восстановить всю таблицу дожития в возрастном интервале 20- 80 лет^*. Прямая проверка данного метода на примере населения Швеции подтвердила, что он действительно позволяет довольно точно восстанавливать таблицы смертности по неполным данным [Гаврилов, 1980]. Приведенный пример показывает также, что практическое значение сходимости к одной точке не зависит от того, существует ли это пересечение реально или же является результатом экстраполяции (аналогично тому, как в оптике параметры мнимого фокуса являются важнейшей характеристикой рассеивающей линзы.

^* (Одного значения интенсивности смертности достаточно в тех случаях, когда величиной фоновой компоненты смертности можно пренебречь (современные данные по развитым странам). В общем случае необходимо знать величину смертности в двух возрастных группах, чтобы учесть существование фоновой смертности.)

Следующий важный вопрос касается достоверности обнаруженного явления. Действительно, приведенные рисунки можно рассматривать лишь как иллюстрацию, но не как доказательство существования компенсационного эффекта смертности. Для доказательства этого явления необходимо показать, что для популяций одного вида закон Гомперца-Мейкема может быть записан следующим образом:

где B - общий для всех популяций возраст, при котором все значения возрастной компоненты смертности становятся равными M. Таким образом 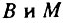- соответственно абсцисса и ордината точки пересечения зависимостей возрастной компоненты смертности от возраста. Как уже отмечалось, величина B была названа видовой продолжительностью жизни, исходя из ее свойства и размерности. Из аналогичных соображений величина M была названа видовой интенсивностью смертности (Гаврилова, 1982; Гаврилов, 1984а).

Нетрудно показать, что пересечение в одной точке возможно в том и только том случае, когда между предэкспоненциальным множителем (R) и показателем экспоненты (α) существует следующая связь:

Действительно, если подставить это соотношение в закон Гомперца- Мейкема, то мы приходим к приведенной выше записи этого закона.

Таким образом, доказательство справедливости компенсационного эффекта смертности сводится к доказательству соотношения (49). Эту проблему можно упростить, если прологарифмировать приведенное выше соотношение:

Итак, доказательство компенсационного эффекта сводится к доказательству существования обратной линейной связи между 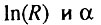, т. е. к задаче, которую в свое время пытались решить Стрелер и Милдван. Однако, как показано в предыдущем разделе, эту задачу необходимо решать заново с учетом фоновой компоненты смертности.

Таблица 9. Характеристики компенсационного эффекта смертности для человека

В табл. 9 приведены результаты такого исследования, выполненного на основе 209 кратких таблиц смертности людей (Гаврилов, 1980; 19846). Видно, что между величинами 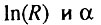существует ярко выраженная обратная связь, близкая к линейной, о чем свидетельствуют значения коэффициентов корреляции, составляющие от -0,92 до -0,95. Интересно отметить, что величина видовой продолжительности жизни, рассчитанная для мужчин (94±3 года) и женщин (96±4 года), оказалась практически одинаковой. Таким образом, есть основания для объединения этих данных и расчета видовой продолжительности жизни человека (95±2 года), общей для мужчин и женщин. Из тех же соображений можно рассчитать единую для мужчин и женщин величину логарифма видовой интенсивности смертности (-0,67±0,21), что соответствует гипотетическому значению возрастной компоненты интенсивности смертности, единому для всех популяций человека в возрасте 95 лет и равному 0,51 года^-1. Вопрос о том, существует ли реально эта точка пересечения и какова динамика смертности после видового возраста, остается пока открытым ввиду недостатка точных данных для старших возрастов. Некоторые гипотезы и наблюдения по этому вопросу можно найти в специальных работах [Гаврилов, 1980; Гаврилова, Гаврилов, 1982]. Необходимо, однако, подчеркнуть, что, независимо от того, существует ли такое пересечение на самом деле, сам факт сходимости большинства зависимостей в одну область все равно будет иметь большое практическое значение (см. выше) и требовать своего теоретического объяснения.

Одно из возможных объяснений компенсационного эффекта смертности, основанное на принципах теории надежности, состоит в том, что скорость первичных процессов разрушения организма при старении является видовой инвариантой. Это на первый взгляд странное утверждение не следует отождествлять с гипотезой запрограммированной смерти, предполагающей существование своеобразной бомбы с часовым механизмом [Коган, 1977]. Просто наличие мощного гомеостаза приводит к тому, что большинство жизненно важных параметров организма, от которых зависит и скорость его разрушения, действительно инвариантны относительно многих воздействий и генетических особенностей. Так, например, температура тела человека составляет примерно 36,7°С и практически не зависит от пола, расовых особенностей и климата мест обитания. Поэтому естественно, что многие процессы разрушения, зависящие от температуры и других подобных факторов, оказываются настолько инвариантными, что по некоторым из них (например, рацемизация L-аминокислот в организме) можно даже оценивать возраст организма [Man ct al., 1983]. Если такое объяснение компенсационного эффекта смертности верно, то для видов с менее мощным гомеостазом, чем у человека (например, для пойкилотермных животных), могут наблюдаться отклонения от данной закономерности.

Таблица 10. Характеристики компенсационного эффекта смертности для Drosophila melanogaster

Действительно, для лабораторных дрозофил компенсационный эффект смертности является скорее исключением, чем правилом. Так, у гибридов первого поколения возрастная зависимость смертности характеризуется параллельным сдвигом по сравнению с соответствующей зависимостью у родительских линий [Sacher, 1977; Гаврилов, 1980], поэтому в данном случае ни о какой сходимости в одну точку говорить не приходится. Тем не менее, как видно из рис. 30 и табл. 10, этот эффект у дрозофил все же иногда наблюдается.

Попытки проверить существование компенсационного эффекта смертности у других биологических видов затруднены из-за отсутствия данных необходимой точности и их малого разнообразия. Действительно, чтобы увидеть сходимость к одной точке и определить ее координаты, необходимо иметь не только точные, но и существенно различающиеся между собой данные по смертности организмов. Поэтому результаты, полученные для лабораторных крыс (табл. 11), следует рассматривать как предварительные, хотя они и свидетельствуют в пользу названного эффекта.

Таблица 11. Характеристики компенсационного эффекта смертности для крыс линии Вистер

Подводя итоги попыткам определения видовой продолжительности жизни, следует признать, что эта проблема оказалась сложнее, чем представлялось ранее. И хотя до сих пор для большинства биологических видов нельзя привести обоснованных оценок видовой продолжительности жизни, сам факт существования видовых инвариант уже не вызывает сомнения. Не исключено, что метод оценки видовых характеристик продолжительности жизни, основанный на законе Гомперца-Мейкема и компенсационном эффекте смертности, окажется не единственно возможным и даже не самым лучшим. Однако сама идея "последовательной экстракции инвариантности" из сырых данных путем поэтапного рассмотрения различного рода зависимостей и корреляций и выделения параметров разной степени общности, по-видимому, будет лежать в основе дальнейших попыток определения видовой продолжительности жизни.