
4.4. Корреляция Стрелера-Милдвана
В 1960 г. в ведущем научном журнале "Science" была опубликована статья с многообещающим названием "Общая теория смертности и старения" [Strehler, Mildvan, 1960]. В этой работе отмечалось, что между параметрами закона Гомперца существует обратная связь: в тех странах, где значения предэкспоненциального множителя (обозначаемого как R0) были высоки, значения показателя экспоненты (α) были понижены. Если же значения, полученные для ряда стран, нанести на один график, то между логарифмом R0 и величиной α наблюдается обратная связь, близкая к линейной. В дальнейшем это наблюдение получило название корреляции Стрелера-Милдвана и приобрело статус фундаментальной закономерности выживаемости организмов [Стрелер, 1964; Strehler, 1977; Халявкин, 1983; 1985].
Нетрудно заметить, что данное явление, если оно действительно существует, имеет важное значение для определения видовых характеристик продолжительности жизни. Действительно, параметры корреляции Стрелера-Милдвана, связывающие между собой величины R0 и α. Уже по самому принципу расчета являются видовыми инвариантами. Поэтому прежде всего возникает вопрос, насколько надежно установлена эта закономерность.
Авторы следующим образом излагают метод своих исследований: "...На полулогарифмическую бумагу были нанесены повозрастные значения вероятности смерти для всех стран, упомянутых в Демографическом ежегоднике ООН за 1955 г. Кривые были гладкими почти для всех стран. Однако в тех немногих случаях, когда наблюдался большой разброс, данные в дальнейшем не анализировались. Через точки от 50 до 70 лет, а в большинстве случаев от 35 до 80 лет были визуально проведены наиболее правдоподобные прямые линии, и значения R0 и а были получены соответственно путем графической экстраполяции и измерения" [Strehler, Mildvan, 1960, p. 21].
В связи с приведенной методикой возникают три замечания.
Прежде всего авторы анализировали не интенсивность смертности, а вероятность смерти. Между тем, как уже отмечалось, экспоненциальный рост характерен именно для интенсивности смертности, а не вероятности смерти. Это замечание, однако, не очень существенно, поскольку для возрастов 35-80 лет численные значения интенсивности смертности и вероятности смерти (в течение года) практически совпадают.
Второе замечание касается качества статистической обработки данных. Действительно, данные анализировались субъективными методами (проведение прямых "на глаз"), в разных возрастных интервалах (то в интервале 50-70 лет, то в интервале 35-80 лет) и без оценки точности определяемых величин (отсутствие доверительных интервалов). Такой способ обработки данных является, безусловно, не самым лучшим из известных даже в то время методов. Впрочем, и это замечание можно считать несущественным по сравнению с последним, третьим замечанием.
В своем исследовании Стрелер и Милдван совершенно игнорировали существование фоновой компоненты смертности, хотя этой величиной нельзя было пренебрегать, особенно в случае следующих использованных авторами таблиц: Алжир (1948 г.), Аргентина (1947 г.). Бразилия (1950 г.), Коста-Рика (1950 г.), Египет (1947 г.) и т.д. Разумеется, когда фоновая компонента смертности равна нулю, анализ данных намного упрощается и сводится к определению параметров линейной зависимости логарифма интенсивности смертности от возраста. Но в данном конкретном случае такое упрощение является совершенно неоправданным, что видно даже из графика, приведенного самими авторами. Так, на рис. 1 в упомянутой статье приведена зависимость логарифма смертности от возраста мужчин Египта в 1947 г. Эту зависимость, имеющую ярко выраженную вогнутую форму, свидетельствующую о высокой фоновой смертности, даже при хорошо развитом воображении нельзя назвать линейной LStrehler, Mildvan, 1960]. Тем не менее, несмотря на то что в начале работы авторы приводят формулу Гомперца-Мейкема, весь дальнейший анализ ведется, исходя из формулы Гомперца. Как будет показано далее, одного только этого "упрощения" достаточно, чтобы породить ложную корреляцию, совпадающую с корреляцией Стрелера-Милдвана.
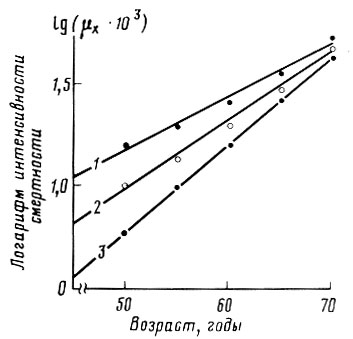
Рис. 27. Влияние фоновой смертности на смещение оценок параметров
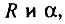 определяемых методом Стрелера и Милдвана. 1 - зависимость логарифма интенсивности смертности от возраста людей при A = 0,010 год-1; 2 - зависимость логарифма интенсивности смертности от возраста людей при A = 0,004 год-1; 3 - зависимость логарифма интенсивности смертности от возраста людей при А = 0,000 год-1. Истинные значения
определяемых методом Стрелера и Милдвана. 1 - зависимость логарифма интенсивности смертности от возраста людей при A = 0,010 год-1; 2 - зависимость логарифма интенсивности смертности от возраста людей при A = 0,004 год-1; 3 - зависимость логарифма интенсивности смертности от возраста людей при А = 0,000 год-1. Истинные значения 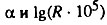 равны соответственно 0,1 год-1 и 0,60
равны соответственно 0,1 год-1 и 0,60
На рис. 27 показано, как выглядят в полулогарифмических координатах зависимости интенсивности смертности от возраста при одних и тех же значениях параметров 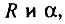 но разной величине параметра A. Можно заметить, что по мере снижения фоновой компоненты смертности (A) зависимость становится все более крутой, что соответствует росту оценки параметра α, определяемого графически по крутизне зависимости. Видно также, что одновременно с этим происходит уменьшение величины отрезка, отсекаемого на оси ординат прямой, проводимой Стрелером и Милдваном через изучаемые зависимости. Это соответствует уменьшению оценки параметра R0. определяемого таким способом. Следовательно, метод определения параметров, использованный Стрелером и Милдваном, приводит к смещению оценок
но разной величине параметра A. Можно заметить, что по мере снижения фоновой компоненты смертности (A) зависимость становится все более крутой, что соответствует росту оценки параметра α, определяемого графически по крутизне зависимости. Видно также, что одновременно с этим происходит уменьшение величины отрезка, отсекаемого на оси ординат прямой, проводимой Стрелером и Милдваном через изучаемые зависимости. Это соответствует уменьшению оценки параметра R0. определяемого таким способом. Следовательно, метод определения параметров, использованный Стрелером и Милдваном, приводит к смещению оценок 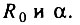 , причем при изменении фоновой компоненты смертности (A) эти оценки смещаются в противоположном направлении, порождая ложную корреляцию.
, причем при изменении фоновой компоненты смертности (A) эти оценки смещаются в противоположном направлении, порождая ложную корреляцию.
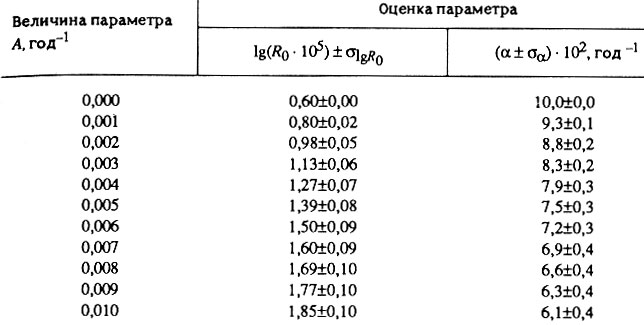 ">
">Таблица 8. Влияние фоновой компоненты смертности на смещение оценок параметров
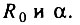
Естественно, возникает вопрос: совпадает ли эта ложная корреляция, связанная с некорректной обработкой данных, с корреляцией Стрелера и Милдвана? Для ответа на этот вопрос был проведен численный эксперимент с использованием типичных значений параметров формулы Гомперца-Мейкема: 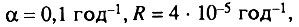
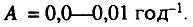 При заданных постоянных значениях параметров
При заданных постоянных значениях параметров 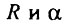 были смоделированы зависимости интенсивности смертности от возраста для целого набора возможных значений параметра A. Затем эти данные обрабатывали в соответствии с методикой Стрелера и Милдвана. Поскольку авторы не указывали, в каких случаях они использовали возрастной интервал линеаризации 35-80 лет, а в каких - 50-70 лет, анализ данных проводился в одном и том же интервале (50-70 лет). В соответствии с методикой этих авторов интервалы между точками составляли 5 лет, так что каждая зависимость содержала по пять точек, соответствующих возрастам 50, 55, 60, 65 и 70 лет. Единственное существенное отличие от методики Стрелера-Милдвана состояло в том, что "линейная" зависимость проводилась не визуально, а методом наименьших квадратов, чтобы исключить субъективность оценок параметров прямой" линии и определить их точность. Результаты проведенных расчетов приведены в табл. 8. Видно, что в зависимости от величины фоновой компоненты смертности наблюдается существенное смещение оценок параметров
были смоделированы зависимости интенсивности смертности от возраста для целого набора возможных значений параметра A. Затем эти данные обрабатывали в соответствии с методикой Стрелера и Милдвана. Поскольку авторы не указывали, в каких случаях они использовали возрастной интервал линеаризации 35-80 лет, а в каких - 50-70 лет, анализ данных проводился в одном и том же интервале (50-70 лет). В соответствии с методикой этих авторов интервалы между точками составляли 5 лет, так что каждая зависимость содержала по пять точек, соответствующих возрастам 50, 55, 60, 65 и 70 лет. Единственное существенное отличие от методики Стрелера-Милдвана состояло в том, что "линейная" зависимость проводилась не визуально, а методом наименьших квадратов, чтобы исключить субъективность оценок параметров прямой" линии и определить их точность. Результаты проведенных расчетов приведены в табл. 8. Видно, что в зависимости от величины фоновой компоненты смертности наблюдается существенное смещение оценок параметров 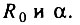 Если же эти результаты сопоставить с данными Стрелера и Милдвана, то они удивительным образом совпадают (рис. 28). Таким образом, корреляция Стрелера-Милдвана не отличается от ложной корреляции, обусловленной некорректностью метода, использованного этими исследователями.
Если же эти результаты сопоставить с данными Стрелера и Милдвана, то они удивительным образом совпадают (рис. 28). Таким образом, корреляция Стрелера-Милдвана не отличается от ложной корреляции, обусловленной некорректностью метода, использованного этими исследователями.
![Рис. 28. Совпадение ложной обратной корреляции между с корреляцией Стрелера-Милдвана. Ложная обратная корреляция, построенная на основании табл. 8, проведена пунктиром. Корреляция Стрелера-Милдвана построена на основании данных, опубликованных в работе [Strehler, Mildvan, 1960]](pic/000142.jpg)
Рис. 28. Совпадение ложной обратной корреляции между
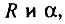 с корреляцией Стрелера-Милдвана. Ложная обратная корреляция, построенная на основании табл. 8, проведена пунктиром. Корреляция Стрелера-Милдвана построена на основании данных, опубликованных в работе [Strehler, Mildvan, 1960]
с корреляцией Стрелера-Милдвана. Ложная обратная корреляция, построенная на основании табл. 8, проведена пунктиром. Корреляция Стрелера-Милдвана построена на основании данных, опубликованных в работе [Strehler, Mildvan, 1960]Приведенный пример показывает, что обсуждение, казалось бы, чисто методических вопросов может приводить к весьма важным выводам. Действительно, корреляция Стрелера и Милдвана широко цитируется без сколь-либо серьезного ее критического анализа [Стрелер. 1964; Strehler, 1977; Doubal, 1982; Кольтовер. 1983; Халявкин, 1983; 1985] и рассматривается даже как фундаментальная закономерность, с которой должна согласовываться любая теория старения, смертности и продолжительности жизни [StrehL r, Mildvan, 1960; Стрелер, 1964; Strehler, 1977]. Между тем попытки использовать корреляцию Стрелера и Милдвана при построении математических моделей старения приводят к абсурдным результатам. Действительно, из данных, приведенных в статье Стрелера и Милдвана [Strehler, Mildvan, 1960], следует, что угловой коэффициент линейной регрессии In R0 и а составляет всего 68,5 года. Между тем в рамках "общей теории смертности и старения" Стрелера и Милдвана эта величина должна соответствовать возрасту, когда так называемая жизненность - "способность отдельного организма оставаться живым" [Ibid., p. 15] - становится равной нулю. Столь же абсурдный результат, что данный параметр, равный 68,5 года, соответствует абсолютному пределу продолжительности жизни человека, вытекает из другой математической модели старения и смертности [Кольтовер, 1983]. На несообразность подобных выводов, вытекающих из корреляции Стрелера-Милдвана, в свое время обращал внимание известный французский демограф Э. Ле Бра [Le Bras, 1976]. Действительно, получается, что величина видового предела продолжительности жизни человека значительно меньше, чем средняя продолжительность жизни населения многих развитых стран. Казалось бы, уже один только этот артефакт должен был насторожить исследователей, работающих в данной области. Этого, к сожалению, не произошло [Стрелер, 1964; Strehler, 1977; Doubal, 1982; Кольтовер, 1983; Халявкин, 1983; 1985], хотя существование противоречия в данном вопросе очевидно и отмечалось неоднократно [Le Bras, 1976; Гаврилови др.. 1978; Гаврилов. 19846].
Поскольку обработка данных в работе Стрелера и Милдвана проводилась субъективным визуальным методом, в 1978 г. была предпринята попытка заново оценить угловой коэффициент изучаемой зависимости, чтобы исключить возможность ошибки и в этом месте [Гаврилов и др., 1978]. Значения параметров 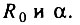 были взяты из той же работы Стрелера и Милдвана (из таблицы, в которой приведены 32 пары значений параметров для мужского населения разных стран мира), и методом наименьших квадратов определена величина углового коэффициента линейной регрессии lnR0 по α. Значение этого коэффициента с соответствующим стандартным отклонением оказалось равным 74±3 года. Хотя рассчитанное значение несколько превышает оценку, полученную Стрелером и Милдваном (68,5 года), оно тем не менее оказывается существенно меньше ожидаемой величины видового предела продолжительности жизни человека.
были взяты из той же работы Стрелера и Милдвана (из таблицы, в которой приведены 32 пары значений параметров для мужского населения разных стран мира), и методом наименьших квадратов определена величина углового коэффициента линейной регрессии lnR0 по α. Значение этого коэффициента с соответствующим стандартным отклонением оказалось равным 74±3 года. Хотя рассчитанное значение несколько превышает оценку, полученную Стрелером и Милдваном (68,5 года), оно тем не менее оказывается существенно меньше ожидаемой величины видового предела продолжительности жизни человека.
Разумеется, выявленное противоречие может быть связано с целым рядом причин: артефактной природой корреляции Стрелера-Милдвана, некорректностью предложенных математических моделей смертности, а также ошибочностью самой концепции абсолютного видового предела длительности жизни. Возможно, что в данном случае все три перечисленные обстоятельства имеют место. Естественно, что сами авторы (Б. Стрелер и А. Милдван) не могли не заметить несогласованности между своей теорией смертности и оценкой видового предела продолжительности жизни, вытекающей из обнаруженной ими корреляции. Однако они не стали акцентировать на этом внимание и быстро перешли к другим приемам оценки величины видового предела, основанным на дополнительных предположениях [Strehler, Mildvan, 1960]. Так. предполагая, что предел продолжительности жизни соответствует возрасту, когда экспоненциально растущая смертность становится равной единице, было рассчитано, что этот предел равен 103 годам. Видно, что и эта оценка существенно меньше огромного числа зарегистрированных рекордов долголетия. К тому же, как можно рассчитать из данных Стрелера-Милдвана [Ibid], эта величина не является видовой инвариантой и сильно варьирует от популяции к популяции, колеблясь в пределах от 90 до 116 лет. Тем не менее в своих дальнейших публикациях авторы больше не возвращались к проверке достоверности описанной корреляции, ссылаясь на нее как на установленный факт [Стрелер, 1964; Strehler, 1977]. Их примеру последовали и другие исследователи [Doubal, 1982; Кольтовер, 1983; Халявкин, 1983; 1985]. Подобная ситуация может показаться несколько странной, но нужно признать, что канонизация артефактов путем длительного некритического цитирования нередко встречается в современной науке.
Таким образом, хотя корреляция Стрелера-Милдвана широко цитируется в научной литературе, ее нельзя считать доказанным научным фактом. Более того, игнорирование этими авторами фоновой компоненты смертности должно было неизбежно породить артефактную зависимость, которая, как мы показали, совпадает с зависимостью, описанной Стрелером и Милдваном. Поэтому корреляция Стрелера-Милдвана непригодна для определения видовых характеристик продолжительности жизни. Тем не менее это не означает, что сама идея поиска видовых инвариант путем сопоставления параметров формулы Гомперца-Мейкема является порочной. Наоборот, как будет показано в следующем разделе, эту идею можно реализовать, если только провести корректную оценку параметров формулы Гомперца-Мейкема.
|
ПОИСК:
|
© GELIB.RU, 2013-2019
При использовании материалов проекта обязательна установка активной ссылки:
http://gelib.ru/ 'Геронтология и гериатрия'
При использовании материалов проекта обязательна установка активной ссылки:
http://gelib.ru/ 'Геронтология и гериатрия'