6.6. Модель резервированной системы с произвольным числом дефектов

В предыдущем разделе была рассмотрена надежностная модель системы, состоящей из m последовательно соединенных блоков, каждый из которых содержит по n параллельно соединенных элементов. Было показано, что поведение этой системы решающим образом зависит от начальных условий. Если система исходно идеальна, т. е. если вероятность q для элементов быть исходно работоспособными равна единице, то модель приводит к степенному закону роста интенсивности смертности (закону Вейбулла). Если же. наоборот, система с самого начала насыщена дефектами, и вероятность элементов быть исходно работоспособными близка к нулю, модель приводит к экспоненциальному закону роста интенсивности смертности (закону Гомперца). В обоих случаях, однако, существует верхний предел роста интенсивности смертности, определяемый произведением числа блоков (m) на интенсивность отказа элементов (k). В данном разделе будет рассмотрен более общий случай, когда вероятность элемента быть исходно работоспособным может принимать любые положительные значения: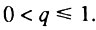

В общем случае распределение блоков в организме по числу исходно работоспособных элементов описывается не законом Пуассона, а биномиальным распределением. Для исходно живого организма это распределение должно быть усечено слева, поскольку, согласно модели, организм, содержащий блок без работоспособных элементов (i = 0) не может быть живым.

Поэтому распределение блоков по числу i исходно работоспособных элементов внутри исходно живых организмов задается следующими значениями вероятности P_i.

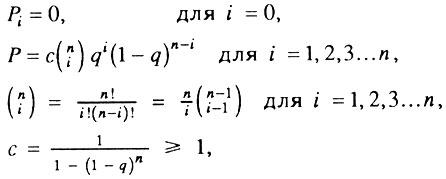
где c - нормирующий множитель, обеспечивающий равенство единице для суммы вероятностей всех событий.

Интенсивность отказов системы, построенной из m последовательно соединенных блоков, равна сумме интенсивностей отказов этих блоков:

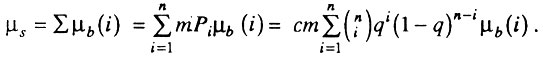
Как уже отмечалось, в начальный момент времени, когда 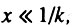интенсивность отказа блока с i исходно работоспособными элементами равна.

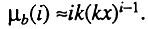
Сопоставляя две приведенные выше формулы, получаем

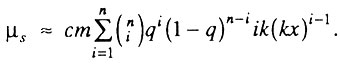
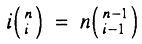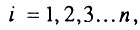Учитывая, что для получаем

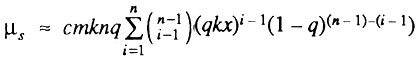
Представленная в этом выражении сумма является биномом Ньютона для выражения 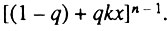Поэтому можно записать:

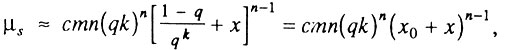
где 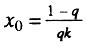- параметр, который мы предлагаем называть начальным виртуальным возрастом системы. Действительно, этот параметр имеет размерность времени и соответствует возрасту, в течение которого исходно идеальная система накопила бы столько дефектов, сколько реальная система уже имеет в начальный момент времени (при x = 0). В частности, когда q = 1, т. е. когда все элементы исходно работоспособны, начальный виртуальный возраст системы равен нулю и интенсивность смертности растет с возрастом по степенному закону (закону Вейбулла), что соответствует случаю, разобранному в Разделе 6.5. В случае же, когда система исходно не идеальна 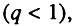мы приходим к так называемому биномиальному закону смертности, впервые предложенному в 1986 г. и упомянутому в разделе 2.4 Данной книги. Таким образом, предложенная здесь обобщенная надежностная модель является теоретическим обоснованием биномиального закона смертности.

В случае, когда 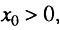всегда существует начальный период времени, такой, что 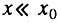и справедливо следующее приближение биномиального закона:

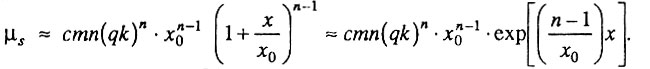
Следовательно, при любом значении 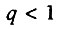всегда существует начальный период времени x, когда число вновь образовавшихся дефектов много меньше их исходного числа, и интенсивность смертности экспоненциально растет с возрастом:

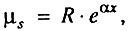
где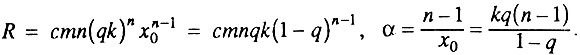

Итак, если система исходно неидеальна (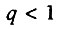), то интенсивность смертности в начальный период времени экспоненциально растет с возрастом (по закону Гомперца).

Обсуждаемая модель позволяет объяснить не только экспоненциальное увеличение интенсивности смертности с возрастом, но и компенсационный эффект смертности, описанный в разделе 4.5. Действительно, согласно введенным обозначениям:

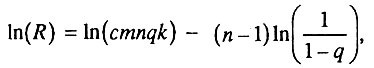
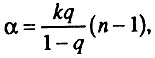
т. е. 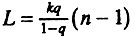величины 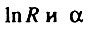параметрически связаны через величину (n - 1). что позволяет представить 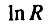как функцию α:

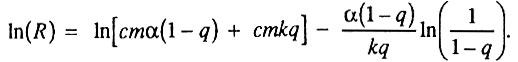
Таким образом, компенсационный эффект смертности наблюдается тогда, когда различия в смертности обусловлены межпопуляционными различиями по числу элементов в блоке (n), а другие параметры, включая скорость старения (скорость необратимой гибели элементов k), практически одинаковы для всех сопоставляемых популяций одного вида. Нетрудно заметить сходство подобного объяснения компенсационного эффекта смертности с объяснением, вытекающим из предыдущей модели, описанной в разделе 6.5.

Следует отметить, что продолжительность периода экспоненциального роста интенсивности смертности зависит от величины q. В общем случае поведение системы на участке возрастов 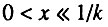в зависимости от величины q может быть сведено к трем сценариям:

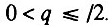1. Данный случай соответствует ситуации, когда исходно работоспособно менее половины общего числа элементов. В этом случае 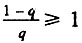и, следовательно, Поэтому во всем интервале, когда 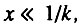всегда выполняется и условие 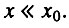В этом случае интенсивность смертности во всем рассматриваемом интервале экспоненциально растет с возрастом.
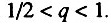2. Данный случай соответствует ситуации, когда исходно работоспособно более половины всех элементов. В этом случае 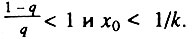В данной ситуации возрастная динамика смертности в исследуемом возрастном интервале 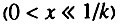состоит из двух стадий:
   • первая стадия начального периода, когда и, следовательно, биномиальный закон смертности сводится к закону Гомперца.
   • вторая стадия начального периода, когда 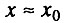и применим только биномиальный закон смертности в полном виде без приближений.
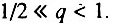3. Данный случай соответствует ситуации, когда исходно дефектна лишь очень небольшая часть элементов. В этом случае 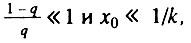а возрастная динамика смертности состоит из трех стадий:
   • первая стадия начального периода, когда 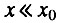и биномиальный закон смертности сводится к закону Гомперца.
   • вторая стадия начального периода, когда 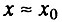и применим только биномиальный закон смертности.
   • третья стадия начального периода, когда 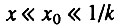и биномиальный закон смертности сводится к степенному закону роста интенсивности смертности (закону Вейбулла).

По мере того как q стремится к единице, продолжительность первой стадии начального периода с экспоненциальным ростом интенсивности смертности стремительно уменьшается, а третьей - стремительно растет. В пределе, в случае исходно идеальной системы (q = 1), мы приходим к закону Вейбулла, справедливому на всем возрастном интервале 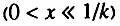. Этот случай уже был описан в разделе 6.5.

Как уже отмечалось, с увеличением возраста интенсивность отказа блоков асимптотически стремится к верхнему пределу интенсивности отказов, не зависящему от числа исходно работоспособных элементов и равному k. Поэтому интенсивность смертности системы, состоящей из m последовательно соединенных блоков, с увеличением возраста асимптотически стремится к верхнему пределу интенсивности смертности, равному шк, независимо от величин пи q.

Таким образом, обсуждаемая надежностная модель позволяет объяснить основные закономерности смертности организмов: экспоненциальный рост интенсивности смертности в начальный период с последующим замедлением темпов ее роста, а также компенсационный эффект смертности. Кроме того, обсуждаемая модель позволяет выяснить условия, при которых наблюдается не экспоненциальный, а степенной закон роста интенсивности смертности (закон Вейбулла). Наконец, предложенная модель позволяет представить два на первый взгляд взаимоисключающих закона - Гомперца и Вейбулла - как частные случаи одного, более общего биномиального закона смертности, получившего в данной модели строгое теоретическое обоснование.

Согласно предложенной модели, судьба неработоспособных элементов и их гибель совершенно не влияют на выводы модели. Поэтому модель будет справедлива и в том случае, если все неработоспособные элементы уже погибнут к моменту формирования взрослого организма, и он будет состоять только из работоспособных элементов (клеток). Важно, что при этом все равно останется след в виде биномиального распределения блоков по числу работоспособных элементов внутри организма Собственно говоря, в этом и состоит суть модели, а рассуждения об исходно дефектных элементах являются лишь одним из возможных обоснований причин вариабельности по степени резервирования. Поэтому предложенная модель может быть названа также моделью последовательно соединенных блоков с варьирующей степенью резервирования.

С учетом сделанных замечаний основной вывод модели может быть переформулирован следующим образом: "Если жизненно важные блоки системы различаются по степени их резервирования, то интенсивность смертности в начальный период времени экспоненциально растет с возрастом (по закону Гомперца)". Это утверждение справедливо при любой форме биномиального распределения блоков в организме по степени их резервирования: с отрицательной (левосторонней) асимметрией. полностью симметричной (нормальный закон распределения), и с положительной (правосторонней) асимметрией. Единственное влияние формы распределения состоит в том, что при отрицательной (левосторонней) асимметрии распределения экспоненциальный рост интенсивности смертности может продолжаться недолго, а в случае симметричного распределения и распределения с положительной асимметрией период экспоненциального роста интенсивности смертности значительно более продолжителен.

Предложенная модель позволяет также устранить противоречие между экспоненциальным ростом интенсивности общей смертности и степенным ростом интенсивности смертности от ряда болезней. Действительно, классификация болезней и причин смерти во многом основана на анатомическом принципе и учете поражения отдельных органов (блоков) организма. Между тем из рассмотренной модели следует, что каждый блок системы отказывает именно по степенному закону, что в итоге приводит к экспоненциальному росту интенсивности общей смертности. Следует, однако, отметить, что подобное объяснение, да и сама модель предполагают исходную однородность организмов по числу содержащихся в них блоков с различной степенью резервирования. Поэтому заслуживает внимания анализ исходно гетерогенной популяции, которому посвящен следующий раздел книги.