6.2. Необходимость критического отношения к математическим моделям продолжительности жизни

Использование математических методов сопряжено с употреблением специфических терминов, правил и критериев, которые зачастую оказываются неизвестными неискушенному читателю. Оказавшись в подобной ситуации, читатель либо отказывается доверять полученным результатам, либо пытается разобраться в способах их получения, либо просто принимает эти результаты на веру. В последнем случае решающим аргументом является факт публикации работы в солидном издании, гарантирующем высокий научный уровень статей путем их тщательного рецензирования.

Ниже будут приведены конкретные примеры, показывающие, что принятие результатов на веру является самым опасным из перечисленных вариантов. Оказывается, что ведущие международные научные издания не обеспечивают надежного заслона публикациям математических моделей продолжительности жизни с очевидными ошибками.

Ниже приведено несколько примеров, которые наглядно свидетельствуют о необходимости самого критического отношения к публикуемым математическим моделям продолжительности жизни и об опасности цитирования выводов подобных работ без их тщательной проверки.

Первый пример пропущенной явной ошибки содержится в работе американского ученого Э. Мэрфи [Murphy, 1978]. В этой работе автор предлагает простую и оригинальную математическую модель старения, названную им моделью Бинго. Согласно данной модели, организм представляет собой систему из к подсистем таких, что выход из строя любой из них приводит к гибели организма. Предполагается, что каждая подсистема выходит из строя после n случайных повреждений, поэтому вероятность того, что подсистема "доживет" до возрастах, записывается следующим образом:

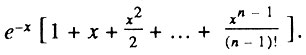
Соответственно для организма вероятность дожить до возраста x равна приведенному выше выражению, возведенному в степень k.

Затем автор дифференцирует полученное выражение по возрасту и получает следующую формулу для плотности вероятности длительности жизни, описывающей распределение организмов по срокам жизни:

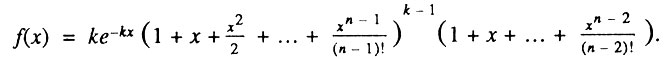
Нетрудно заметить, что в данном случае совершена типичная ошибка: продифференцирован только один сомножитель произведения, а экспоненциальный сомножитель оставлен без изменения так, как если бы эта величина была постоянной. Если же продифференцировать формулу правильно, то она преобразуется в совсем другое, более простое выражение.

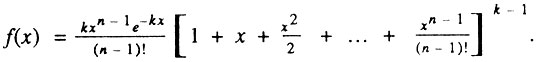
В ответе на наш письменный запрос автор обсуждаемой модели признал факт существования ошибки и объяснил ее опечаткой, допущенной издательством. Поскольку для читателя гораздо важнее узнать не конкретного виновника этой странной опечатки, а правильную формулу, то приведенный пример указывает на необходимость тщательной самостоятельной проверки всех выкладок публикуемых математических моделей.

Другой пример относится к математической модели, опубликованной в международном геронтологическом журнале "Mechanisms of Ageing and Development" [Skurnick, Kemeny, 1978a]. Данная модель насыщена большим количеством математических символов и терминов и способна произвести шокирующее впечатление на большинство биологов и медиков. Действительно, в работе используется достаточно сложный и специфический аппарат статистики экстремальных значений, рассматриваются типы предельных распределений экстремальных значений и условия сходимости к тому или иному предельному распределению.

Авторы данной модели считают, что организм можно уподобить цепи, прочность которой определяется прочностью самого слабого звена. Таким образом, организм, составленный из n связей, погибает, как только порвется первая связь. Нетрудно заметить, некоторое сходство этой модели с уже упомянутой моделью Бинго (n связей организма в ней соответствует к подсистемам организма в предыдущей модели). Основное отличие модели в том, что число n считается таким большим, что можно переходить к предельным распределениям наименьших значений (поскольку время жизни организма определяется наименьшим временем "жизни" самой слабой связи). Процесс разрушения связей является случайным последовательным процессом накопления повреждений до их критического числа, равного α. На основании сделанных предположений авторы приходят к выводу, что в начальный период жизни интенсивность смертности должна расти с возрастом по степенному закону (закон Вейбулла), а затем, в области больших возрастов. - по закону геометрической прогрессии (закон Гомперца). Обоснование первой части этого вывода хорошо известно специалистам по статистике экстремальных значений [Барлоу. Прошан, 1984]. Вторая же часть вывода ошибочна, поскольку авторы модели при поиске распределения наименьших значений механически используют критерий сходимости к распределению наибольших значений:

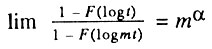
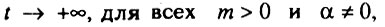
где 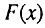- функция распределения времени жизни связей организма.

Данная ошибка тем более удивительна (что хорошо известно [Барлоу, Прошан. 1984; Галамбош, 1984] и совершенно очевидно даже из интуитивных соображений), что вид распределения наименьших значений следует искать также в области наименьших значений, а не при 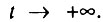Данная ошибка свидетельствует о том, что авторы модели, добросовестно изложив основные положения статистики экстремальных значений, сами не разобрались до конца в сути излагаемой теории. Приведенный пример показывает также, что даже ведущий международный журнал не может обеспечить квалифицированного рецензирования работ по математическому моделированию продолжительности жизни. Читателям же. запутавшимся в дебрях математической символики, можно порекомендовать шире опираться на интуицию и здравый смысл, которые помогают найти возможные ошибки в математических моделях старения. Что касается применения статистики экстремальных значений для моделирования продолжительности жизни, то этот вопрос будет рассмотрен подробно в разделе 6.3 данной главы.

Публикации некорректных математических моделей продолжительности жизни нередко встречаются и в советских научных изданиях. Так, в научном журнале "Успехи современной биологии", а также в шести других изданиях была опубликована одна и та же математическая модель, содержащая, как оказалось, целый набор явных логических противоречий [Гаврилов, 1987].

Автор модели [Кольтовер, 1983] предполагает, что смерть многоклеточного организма (в том числе и человека) всегда наступает в результате повреждения хотя бы одного из Q блоков генов в геноме. При этом совершенно упускается из виду, что геном содержится почти в каждой клетке организма! В результате все выкладки математической модели оказываются основаны на скрытом допущении, что смерть многоклеточного организма наступает тогда и только тогда, когда повреждается один особый геном (клетка) во всем организме. Повреждение же всех остальных клеток в организме, согласно данной модели, не оказывает никакого влияния на его жизнеспособность! Несостоятельность такого скрытого предположения модели очевидна, поскольку "предложенная математическая модель скорее соответствует сказке о Кощее Бессмертном, чья смерть действительно была локализована в одном яйце" [Гаврилов, 1988а]. Далее, автор модели приписывает каждому j-му блоку в особом геноме определенную величину так называемой "дисфункции", равную 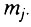Постулируется, что время безотказной работы блока определяется формулой.

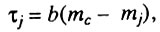
где m_c - критическая величина "дисфункции", одинаковая для всех блоков. Таким образом, из данной модели следует, что продолжительность жизни организма с абсолютной точностью определяется его состоянием (наибольшей из величин "дисфункций") в начальный момент времени. Эта детерминированная модель фатальной предопределенности длительности жизни преподносится автором как "вероятностная модель старения", а величина ту, строго детерминированно (линейно) растущая с возрастом, объявляется случайной величиной (Кольтовер, 1983].

Поскольку данная "вероятностная модель" приводит к одномоментному вымиранию однородной популяции, автор модели вводит гипотезу о гетерогенности популяции по исходной величине "дисфункции". Делается это следующим образом: "Так как для сложных систем характерен экспоненциальный закон распределения времени безотказной работы, то было предположено, что совокупность величин m_j представляет собой случайную выборку из усеченного экспоненциального распределения". В результате автор получает желаемое распределение с возрастающей интенсивностью смертности, т. е. распределение времени жизни стареющих организмов. Читатель же становится свидетелем логического "чуда": из отсутствия старения выводится существование старения! Однако при более внимательном рассмотрении можно заметить, что это "чудо" построено на игре слов, поскольку между экспоненциальным законом распределения времени безотказной работы и усеченным экспоненциальным распределением по величине "дисфункции" нет ничего общего, если не считать слова "экспоненциальный". Кроме того, как выяснилось, эта модель, состоящая из взаимоисключающих утверждений, не согласуется и с реальными данными [Гаврилов, 1984а. 19846; Гаврилов и др.. 1984].

Занимательный пример математических преобразований содержится в модели Виттена [Witten, 1985], опубликованной в уже упоминавшемся международном журнале "Mechanisms of Ageing and Development". Автор исходит из предположения, что функция распределения времени жизни элемента системы следует экспоненциальному закону с параметром α:

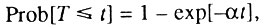
причем и из текста статьи и здравого смысла следует, что α>0 (в противном случае вероятность была бы отрицательной). Затем следует серия преобразований и выводится закон Гомперца в виде:

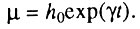
Самое удивительное в этой работе состоит в том, что параметр γ вводится следующим образом:

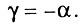
Нетрудно заметить, что параметры 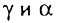не могут быть одновременно положительными, хотя только в этом случае предложенная модель заслуживала бы внимания.

Разумеется, приведенные примеры не следует обобщать на все математические модели продолжительности жизни и ставить под сомнение плодотворность математического моделирования в целом. Цель рассмотрения приведенных примеров состоит лишь в том. чтобы предупредить читателя о необходимости критического отношения к математическим моделям продолжительности жизни, где бы они ни были опубликованы.